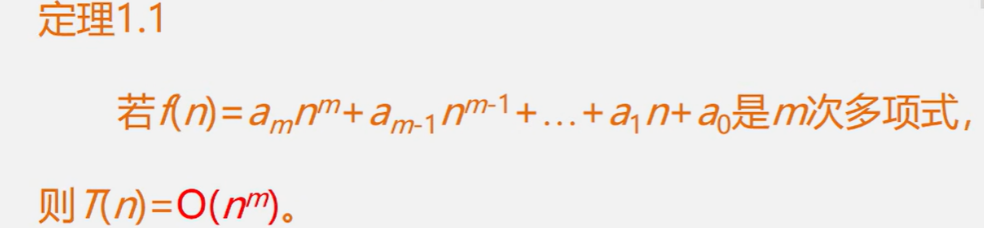绪论
数据
- 数值型数据:整数,实数
- 非数值型数据:文字、图像、图形、声音
由数据元素组成
数据元素
数据的基本单位:元素,记录,结点,顶点
是集合的个体
数据项
构成数据元素的不可分割的最小单位
数据对象
性质相同的数据元素的集合,数据的一个子集
数据结构
数据元素相互之间的关系称为结构
数据结构是带结构的数据元素的集合
数据结构包括:
- 数据的逻辑结构(数据元素之间的逻辑关系)
- 数据的存储结构(数据元素及其关系在计算机内存中的表示-映像)
- 数据的运算和实现(对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现)
数据结构的两个层次
逻辑结构
数据元素之间的逻辑关系
与数据的存储无关,独立于计算机
是从具体问题抽象出来的数学模型
存储结构
数据元素及其关系在计算机存储器中的结构
两者关系
存储结构是逻辑关系的映像与元素本身的映像
逻辑结构是数据皆否的抽象,存储结构是数据结构的实现
逻辑结构的种类
1.线性结构
线性表,栈,队列,串
1.非线性结构
树,图
2.集合结构
2.线性结构
2.树形结构
2.图状结构
四种基本的存储结构
顺序存储结构:连续存储单元存储数据
链式存储结构:任意存储单元存储数据,指针
索引存储结构:建立附加索引表
散列存储结构(哈希):根据关键字计算出位置
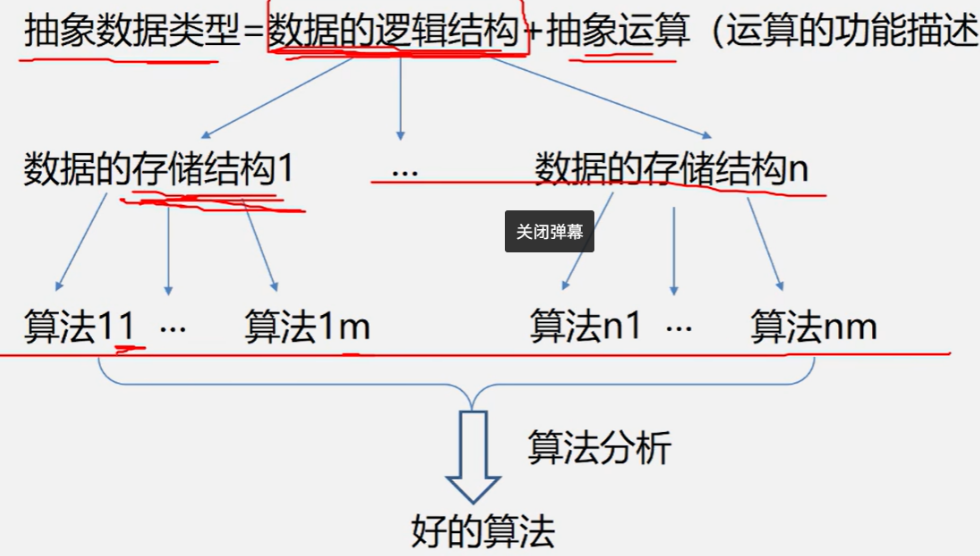
数据类型
数据类型是一组性质相同的值的集合以及定义于这个值集合上的一组操作的总称
数据类型=值的集合+值集合上的一些操作
int,char,float,double等基本数据类型
数组,结构,共用体,枚举等构造数据类型
指针,空类型
typedef自定义数据类型
数据类型约束了常量或变量的取值范围和操作
抽象数据类型(ADT)
是指一个数据模型以及定义在此数据模型上的一组操作
(不考虑在计算机内部的具体存储结构与运算的具体实现算法)
抽象数据类型的形式定义
D S P(D是数据对象,S是D上的关系集,P是对D的基本操作集)
数据对象,数据关系的定义用伪代码描述
1
2
3
4
5
| ADT 抽象数据类型名{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}ADT 抽象数据类型名
|
基本操作的定义格式:
- 基本操作名(参数表)为操作提供输入值,引用参数以&打头,除了可以提供输入值外,还将返回操作结果
- 初始条件:(初始条件描述)描述操作执行之前数据结构和参数应该满足的条件,若不满足则操作失败,并返回相应出错消息,若初始条件是空,则省略
- 操作结果:(操作结果描述)如果操作正常完成之后,数据结构的变化状况和应该返回的结果



抽象数据类型可以通过固有的数据类型(如整型,实型,字符型)来表示和实现
注:可以使用类C语言(介于伪码和C语言之间)作为描述工具


算法
对特定问题求解方法和步骤的一种描述,是指令的有限序列
算法的描述
- 自然语言:英语,中文
- 流程图:传统流程图,NS流程图
- 伪代码,类语言:C语言
- 程序代码:
算法与程序
一个问题可以有多种算法
程序是用某种程序设计语言对算法的具体实现
算法特性
- 有穷性
- 确定性
- 可行性
- 零个或多个输入
- 一个或者多个输出
算法设计的要求
算法效率
算法时间效率的度量
算法时间效率可以用依据该算法变只的程序在计算机上执行所消耗的时间来度量
- 事后统计
- 事前分析:算法运行时间=一个简单操作所需的时间*简单操作次数

(每条语句的执行次数也叫语句频度)
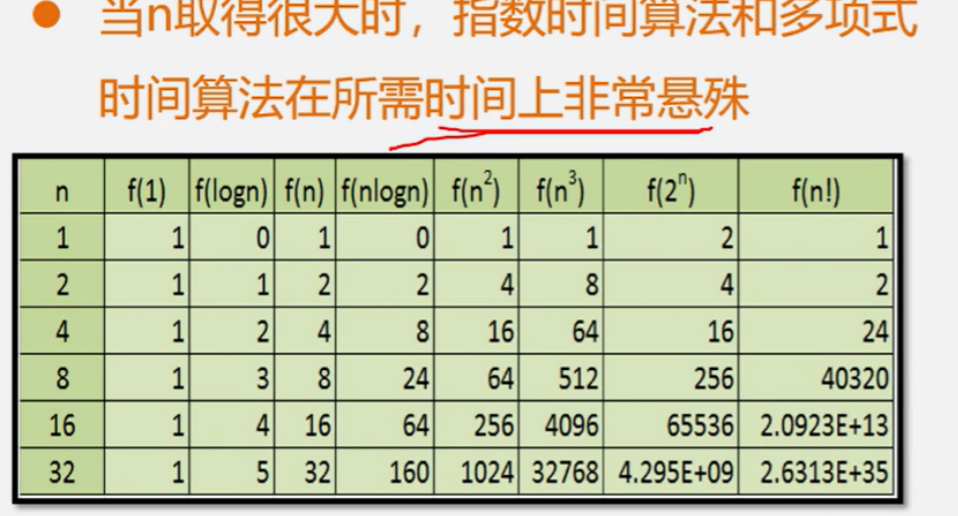
算法运行时间只考虑语句频度即可
最终只比较数量级(最高项):算法时间复杂度的渐进表示法
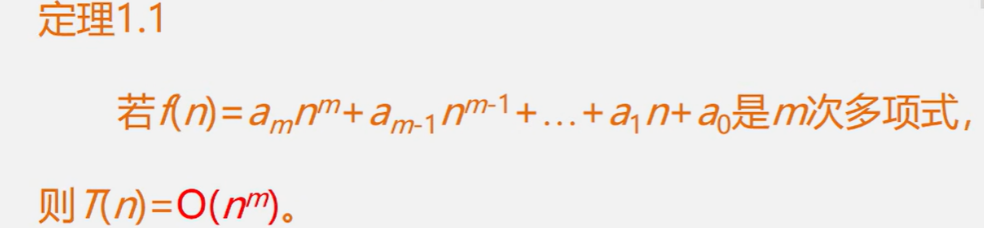
- 最坏时间复杂度
- 平均时间复杂度
- 最好时间复杂度(一般考虑最坏和平均)


算法空间效率的度量
空间复杂度:算法所需存储空间的度量



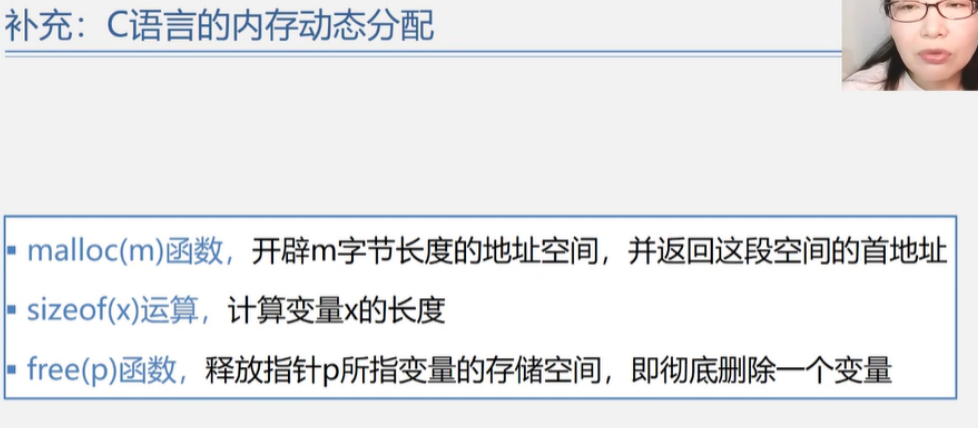
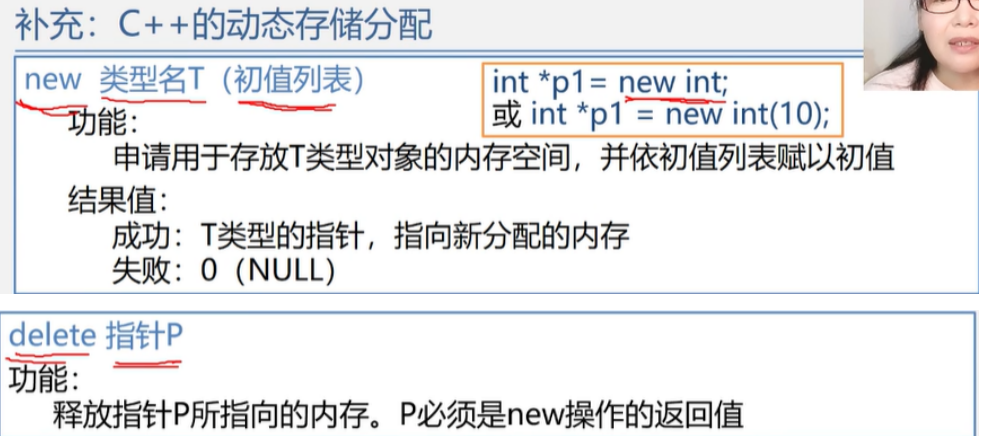
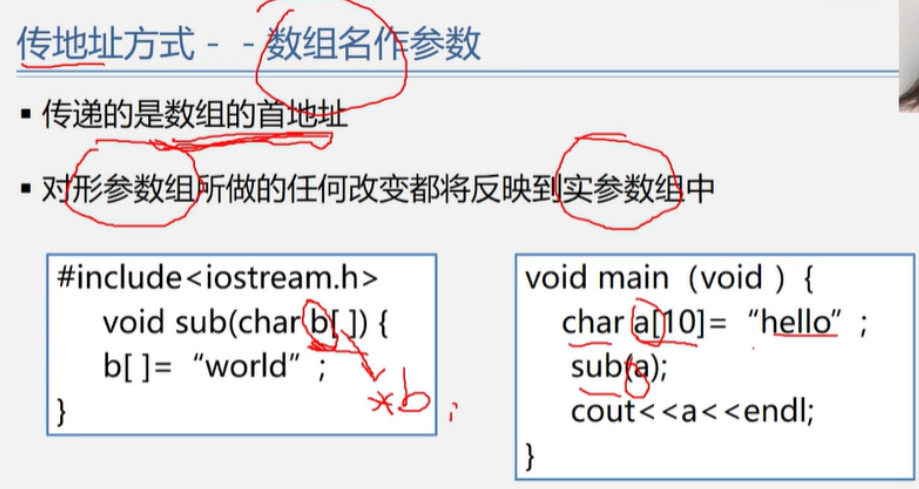
类C语言操作







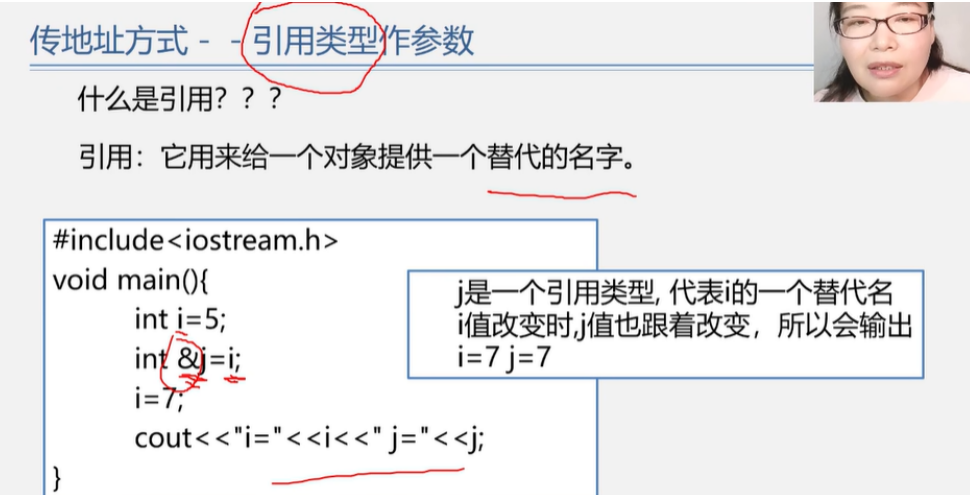


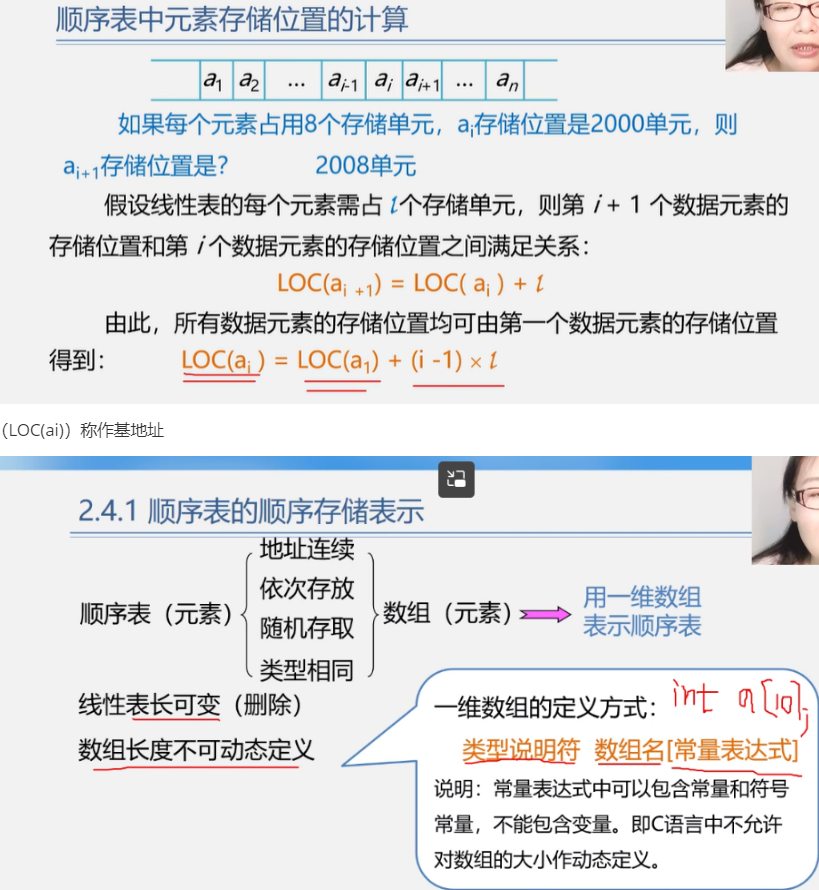
线性表
线性表的定义和特点
线性表是具有相同特性的数据元素的一个有限序列
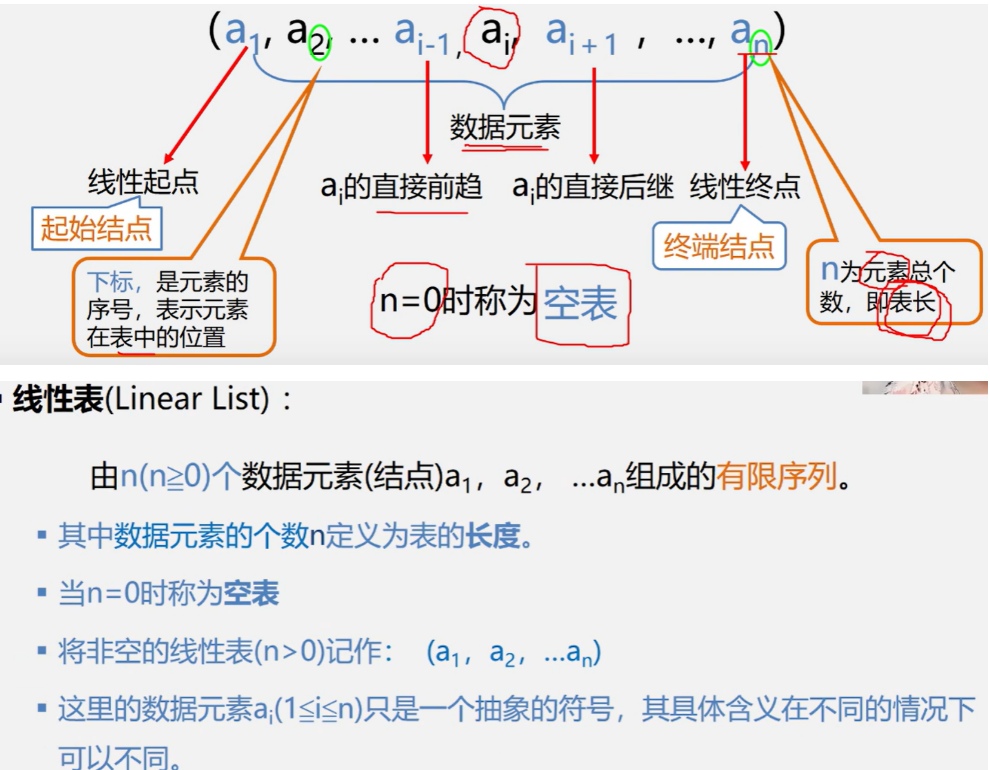

线性表的案例引入
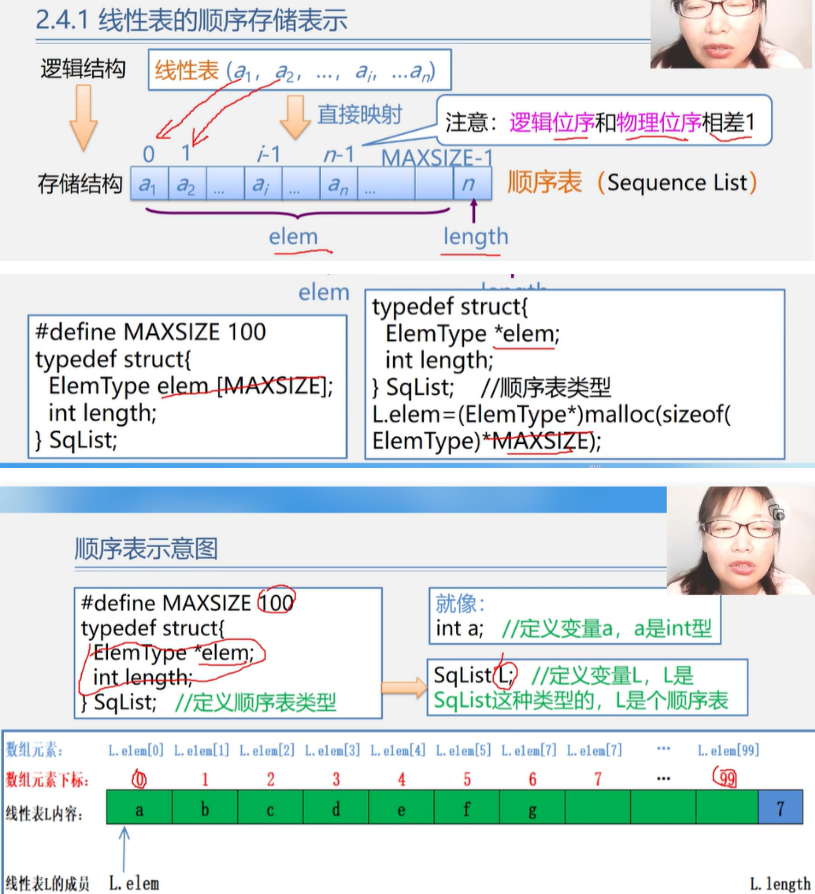
线性表的类型定义


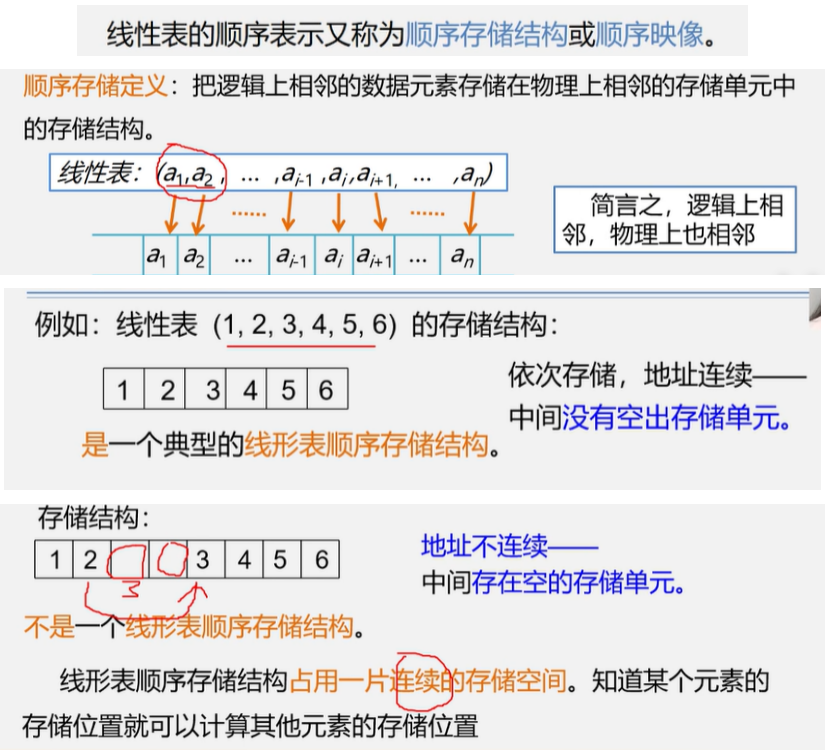
线性表的顺序表示和实现
(线性表有顺序存储结构和链式存储结构)

1
2
3
4
5
| #define LIST_INIT_SIZE 100
typedef struct{
ElemType elem[LIST_INIT_SIZE];
int length;
}SqlList;
|

eg
1
2
3
4
5
6
7
8
9
| #define MAXSIZE 1000
typedef struct {
float p;
float e;
}Polynomial;
typedef struct{
Polynomial *elem;
int length;
}SqList;
|
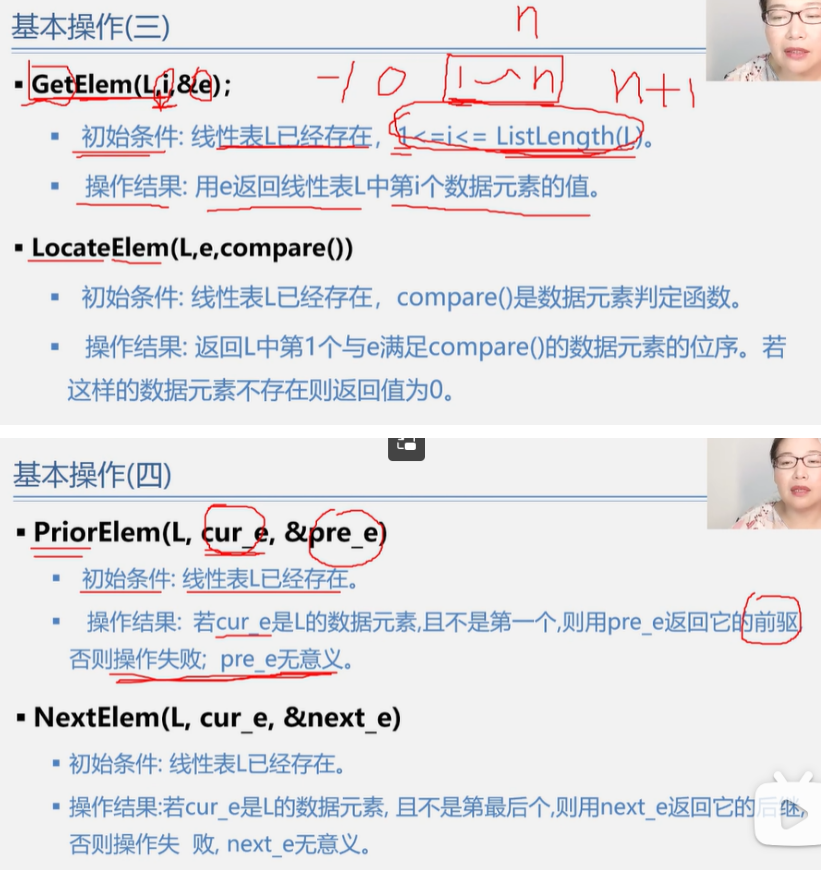
线性表的基本操作
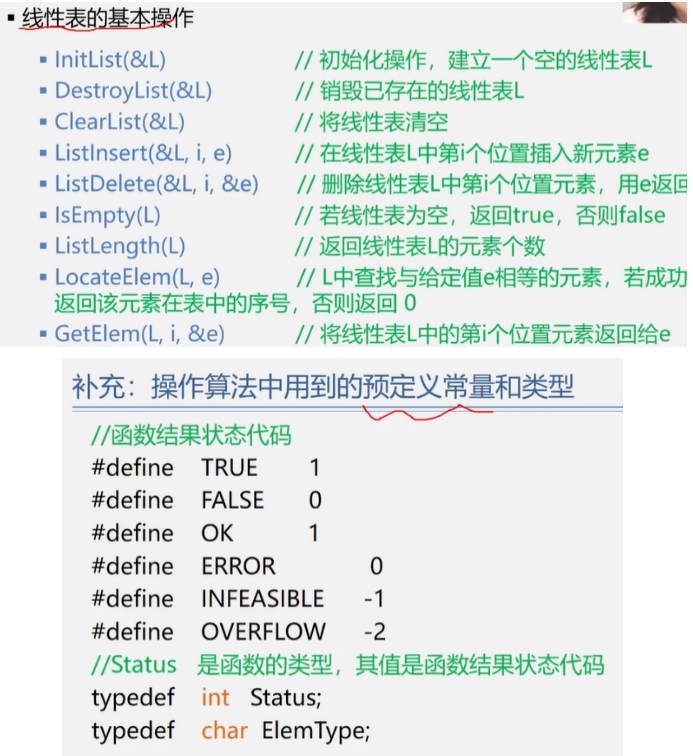
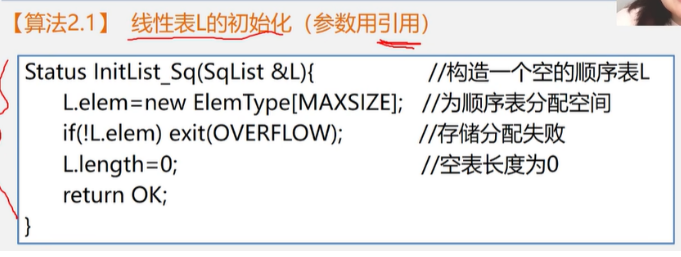
线性表的初始化
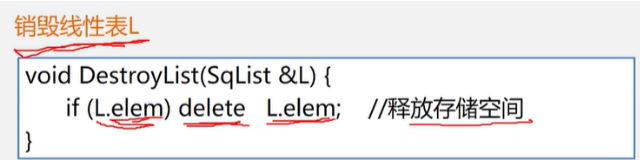
销毁线性表
清空线性表

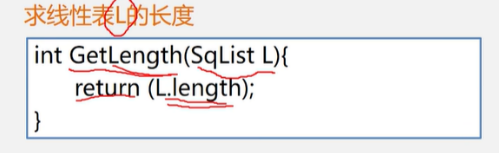
求线性表的长度
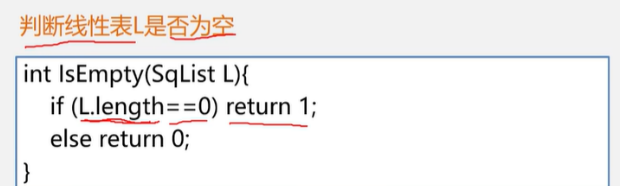
判断线性表是否为空
顺序表的取值

按值查找
链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
| void InitList(LinkNode*& L)
{
L = (LinkNode*)malloc(sizeof(LinkNode));
L->next = NULL;
}
void CreateListR(LinkNode*& L, ElemType a[],int n)
{
LinkNode* s,*r;
L=(LinkNode*)malloc(sizeof(LinkNode));
r = L;
for (int i = 0; i < n; i++)
{
s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = a[i];
r->next = s;
r = s;
}
r->next = NULL;
}
void CreateListF(LinkNode*& L, ElemType a[], int n)
{
LinkNode* s;
L = (LinkNode*)malloc(sizeof(LinkNode));
L->next = NULL;
for (int i = 0; i < n; i++)
{
s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = a[i];
s->next = L->next;
L->next = s;
}
}
void DestroyList(LinkNode *&L)
{
LinkNode *pre=L,*p=L->next;
while(p!=NULL)
{
free(p);
pre=p;
p=pre->next;
}
free(pre);
}
bool ListEmpty(LinkNode *L)
{
return (L->next==NULL);
}
int ListLength(LinkNode *L)
{
int n=0;
LinkNode *p=L;
while(p->next!=NULL)
{
n++;
p=p->next;
}
return (n);
}
void DispList(LinkNode *L)
{
LinkNode *p=L->next;
while(p!=NULL)
{
printf("%d",p->data);
p=p->next;
}
printf("
");
}
bool GetElem(LinkNode *L,int i,ElemType &e)
{
int j=0;
LinkNode *p=L;
if(i<=0) return false;
while(j<i&&p!=NULL)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
e=p->data;
return true;
}
}
int LocateElem(LinkNode *L,ElemType e)
{
int i=1;
LinkNode *p=L->next;
while(p!=NULL&&p->data!=e)
{
p=p->next;
i++;
}
if(p==NULL)
return (0);
else
return (i);
}
bool ListInsert(LinkNode *& L,int i,ElemType e)
{
int j=0;
LinkNode *p=L,*s;
if(i<=0)return false;
while(j<i-1&&p!=NULL)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
s=(LinkNode*)malloc(sizeof(LinkNode));
s->data=e;
s->next=p->next;
p->next=s;
return true;
}
}
bool ListDelete(LinkNode *& L,int i,ElemType & e)
{
int j=0;
LinkNode *p=L,*q;
if(i<=0)return false;
while(j<i-1&&p!=NULL)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
q=p->next;
if(q==NULL)
return false;
e=q->data;
p->next=q->next;
free(q);
return true;
}
}
|